[정리] 모두를 위한 딥러닝 06 - Softmax Regression (Multinomial Logistic Regression) by 김성훈
강의 웹사이트 : http://hunkim.github.io/ml/
Lec = 강의 / Lab = 실습
결과값이 A, B, C 중에 하나인 경우, 지금까지 알아본 내용(리니어 리그리션)으로는 불가능합니다.
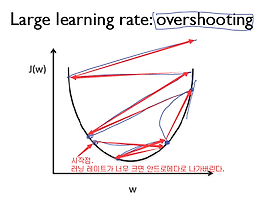
시그모이드 개념과 비슷하긴 하지만, 이 함수는 둘 중 하나로 수렴하기 때문에,
결과가 3개 넘을때에는 이중에서 하나로 수렴할 수 있는 방법이 없습니다.
A, B, C 가 나올 확률을 구해서 가장 높은거 하나만 1, 나머지는 0 으로 만들면 됩니다.
A, B, C 가 나올 확률의 합은 1 이 됩니다.
입력 X, 결과 Y 모두 행렬을 이용하는데, 이 개념이 소프트맥스 softmax 입니다.
이를 위해 로그함수를 두번 사용하면 가능하며, 더 발전된 원핫 인코딩 One-Hot 함수를 사용하면 좋습니다.
실제 소스 코드는 아래와 같습니다.
x_data = [[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5],
[1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]]
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]]
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
nb_classes = 3
W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
# Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}))
-----------------------------------------------------------------------------
파일에서 불러와서 원핫 인코딩을 사용하는 샘플
# Predicting animal type based on various features
xy = np.loadtxt('data-04-zoo.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
nb_classes = 7 # 0 ~ 6
X = tf.placeholder(tf.float32, [None, 16])
Y = tf.placeholder(tf.int32, [None, 1]) # 0 ~ 6
Y_one_hot = tf.one_hot(Y, nb_classes) # one hot
Y_one_hot = tf.reshape(Y_one_hot, [-1, nb_classes])
W = tf.Variable(tf.random_normal([16, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
logits = tf.matmul(X, W) + b
hypothesis = tf.nn.softmax(logits)
# Cross entropy cost/loss
cost_i = tf.nn.softmax_cross_entropy_with_logits(logits=logits,
labels=Y_one_hot)
cost = tf.reduce_mean(cost_i)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
cost = tf.reduce_mean(cost_i)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
prediction = tf.argmax(hypothesis, 1)
correct_prediction = tf.equal(prediction, tf.argmax(Y_one_hot, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2000):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 100 == 0:
loss, acc = sess.run([cost, accuracy], feed_dict={
X: x_data, Y: y_data})
print("Step: {:5}\tLoss: {:.3f}\tAcc: {:.2%}".format(
step, loss, acc))
# Let's see if we can predict
pred = sess.run(prediction, feed_dict={X: x_data})
# y_data: (N,1) = flatten => (N, ) matches pred.shape
for p, y in zip(pred, y_data.flatten()):
print("[{}] Prediction: {} True Y: {}".format(p == int(y), p, int(y)))
소스코드 다운로드 : https://github.com/hunkim/DeepLearningZeroToAll
'Tech > 머신러닝' 카테고리의 다른 글
| [정리] 모두를 위한 딥러닝 07 - 실전 연습 및 팁 by 김성훈 (0) | 2018.06.15 |
|---|---|
| [정리] 모두를 위한 딥러닝 08 - 딥러닝 개념 by 김성훈 (0) | 2018.06.15 |
| 케라스 Keras 모델 저장, 재사용 (0) | 2018.06.12 |
| [정리] 모두를 위한 딥러닝 10 - 렐루 ReLU & 초기값 정하기 by 김성훈 (0) | 2018.06.12 |
| [정리] 모두를 위한 딥러닝 09 - XOR 풀기 by 김성훈 (0) | 2018.06.11 |